Which Three Statements May Correctly Explain Why The Population Size Increases After Time Point C?

In the following example, we illustrate the sampling distribution for the sample mean for a very small population. The sampling method is done without replacement.

Sample Ways with a Minor Population: Pumpkin Weights

Image of pumpkins

In this example, the population is the weight of half-dozen pumpkins (in pounds) displayed in a carnival "approximate the weight" game booth. Y'all are asked to guess the boilerplate weight of the six pumpkins by taking a random sample without replacement from the population.

Pumpkin	A	B	C	D	E	F
Weight (in pounds)	xix	14	15	ix	10	17

Since we know the weights from the population, we can find the population mean.

\(\mu=\dfrac{xix+fourteen+15+9+10+17}{6}=fourteen\) pounds

To demonstrate the sampling distribution, let'due south start with obtaining all of the possible samples of size \(n=2\) from the populations, sampling without replacement. The table below shows all the possible samples, the weights for the chosen pumpkins, the sample hateful and the probability of obtaining each sample. Since we are drawing at random, each sample will accept the aforementioned probability of being chosen.

Sample	Weight	\(\boldsymbol{\bar{ten}}\)	Probability
A, B	19, fourteen	16.v	\(\frac{ane}{xv}\)
A, C	xix, 15	17.0	\(\frac{1}{15}\)
A, D	19, 9	14.0	\(\frac{1}{15}\)
A, East	nineteen, 10	xiv.5	\(\frac{1}{xv}\)
A, F	19, 17	18.0	\(\frac{1}{xv}\)
B, C	14, 15	xiv.5	\(\frac{1}{xv}\)
B, D	14, nine	11.5	\(\frac{i}{15}\)
B, E	14, 10	12.0	\(\frac{ane}{fifteen}\)
B, F	14, 17	15.5	\(\frac{1}{fifteen}\)
C, D	fifteen, 9	12.0	\(\frac{i}{15}\)
C, E	15, 10	12.5	\(\frac{one}{15}\)
C, F	xv, 17	16.0	\(\frac{i}{15}\)
D, E	9, x	nine.5	\(\frac{1}{xv}\)
D, F	9, 17	13.0	\(\frac{1}{xv}\)
East, F	10, 17	13.5	\(\frac{ane}{15}\)

We tin combine all of the values and create a tabular array of the possible values and their respective probabilities.

\(\boldsymbol{\bar{10}}\)	ix.5	11.v	12.0	12.five	13.0	13.5	xiv.0	fourteen.5	15.5	16.0	xvi.5	17.0	eighteen.0
Probability	\(\frac{1}{15}\)	\(\frac{i}{15}\)	\(\frac{two}{15}\)	\(\frac{1}{15}\)	\(\frac{1}{xv}\)	\(\frac{1}{15}\)	\(\frac{1}{15}\)	\(\frac{2}{fifteen}\)	\(\frac{1}{15}\)	\(\frac{1}{15}\)	\(\frac{i}{xv}\)	\(\frac{ane}{xv}\)	\(\frac{1}{fifteen}\)

The table is the probability table for the sample mean and information technology is the sampling distribution of the sample hateful weights of the pumpkins when the sample size is 2. It is too worth noting that the sum of all the probabilities equals 1. It might be helpful to graph these values.

Sampling Distribution

1 can run into that the chance that the sample mean is exactly the population mean is only 1 in 15, very pocket-sized. (In some other examples, it may happen that the sample mean tin can never be the same value as the population hateful.) When using the sample mean to approximate the population hateful, some possible error will exist involved since the sample mean is random.

Now that we have the sampling distribution of the sample hateful, we tin can calculate the mean of all the sample means. In other words, we can find the mean (or expected value) of all the possible \(\bar{10}\)'s.

The mean of the sample means is

\(\mu_\bar{ten}=\sum \bar{10}_{i}f(\bar{x}_i)=9.five\left(\frac{1}{15}\right)+xi.5\left(\frac{1}{xv}\right)+12\left(\frac{2}{fifteen}\correct)\\+12.5\left(\frac{1}{15}\right)+13\left(\frac{ane}{15}\right)+13.5\left(\frac{one}{15}\right)+14\left(\frac{1}{fifteen}\correct)\\+xiv.5\left(\frac{2}{xv}\right)+xv.5\left(\frac{1}{fifteen}\right)+sixteen\left(\frac{1}{fifteen}\right)+16.5\left(\frac{1}{xv}\right)\\+17\left(\frac{1}{xv}\right)+eighteen\left(\frac{1}{15}\right)=fourteen\)

Even though each sample may give you an respond involving some error, the expected value is correct at the target: exactly the population mean. In other words, if one does the experiment over and over again, the overall average of the sample mean is exactly the population mean.

Now, let's do the aforementioned thing as above but with sample size \(n=5\)

Sample	Weights	\(\boldsymbol{\bar{x}}\)	Probability
A, B, C, D, E	19, 14, 15, nine, 10	13.4	one/6
A, B, C, D, F	19, 14, 15, 9, 17	fourteen.8	ane/six
A, B, C, E, F	nineteen, 14, 15, ten, 17	fifteen.0	1/6
A, B, D, Eastward, F	19, 14, nine, x, 17	xiii.8	1/6
A, C, D, Eastward, F	19, fifteen, 9, 10, 17	14.0	1/half dozen
B, C, D, Eastward, F	xiv, 15, 9, 10, 17	xiii.0	1/half-dozen

The sampling distribution is:

\(\boldsymbol{\bar{10}}\)	thirteen.0	13.4	thirteen.8	14.0	14.viii	fifteen.0
Probability	one/half-dozen	1/half-dozen	1/6	1/6	1/6	1/vi

The mean of the sample ways is...

\(\mu=(\dfrac{1}{6})(xiii+13.iv+13.viii+xiv.0+xiv.8+15.0)=xiv\) pounds

The following dot plots show the distribution of the sample means corresponding to sample sizes of \(north=two\) and of \(n=5\).

Population Mean

Again, nosotros see that using the sample hateful to estimate population hateful involves sampling mistake. However, the error with a sample of size \(n=five\) is on the average smaller than with a sample of size \(n= 2\).

Sampling Error and Size

Sampling Error: The error resulting from using a sample feature to estimate a population characteristic.

Sample size and sampling error: As the dotplots higher up evidence, the possible sample means cluster more closely around the population mean as the sample size increases. Thus, the possible sampling error decreases as sample size increases.

What happens when the population is non small, equally in the pumpkin example?

Sample Means with Large Samples: Test Case

Exam scores banner image

An teacher of an introduction to statistics grade has 200 students. The scores out of 100 points are shown in the histogram.

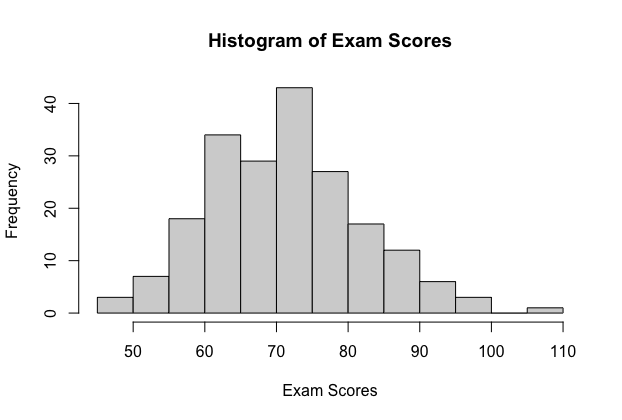
The population hateful is \(μ=71.18\) and the population standard divergence is \(σ=10.73\)

Let's demonstrate the sampling distribution of the sample means using the StatKey website. The first video will demonstrate the sampling distribution of the sample mean when north = 10 for the examination scores data. The second video will show the aforementioned information but with samples of n = thirty.

n=ten
n=xxx

You should start to come across some patterns. The mean of the sampling distribution is very shut to the population mean. The standard deviation of the sampling distribution is smaller than the standard divergence of the population.

In the examples so far, we were given the population and sampled from that population.

What happens when we practice not take the population to sample from? What happens when all that we are given is the sample? Fortunately, we can use some theory to aid u.s.a.. The mathematical details of the theory are across the scope of this course simply the results are presented in this lesson.

In the next two sections, nosotros will hash out the sampling distribution of the sample mean when the population is Normally distributed and when it is not.